Visiting the Tiny World of the Qubit and Beyond

Qubit Modalities, Computational Advantage, Ideal Qubits, and P-bits

Jun 08, 2022

This week, The Social Qubit would like to speak of the tiny world of the qubit and the kind of work that has been done to make qubits stable enough for quantum computers. In addition, after giving the nod to some very public quantum advantage, we would like to draw attention to last month’s exciting news of a potential first ideal qubit. Lastly, and very excitingly, we look a bit beyond quantum’s purview, to discuss the poor man’s qubit, otherwise known as the p-bit.

Qubit Modalities

As you may know, the qubit is the smallest unit of a quantum computer that transmits information. Qubits are drawn from various materials, each representing a specific modality with different computational performance characteristics for the following properties: coherence time, gate fidelity, gate time, scalability, and quantum error correction.

The coherence time corresponds to how long a qubit can survive in a superposition state before decoherence occurs. When employing algorithms, it is critical that the coherence time exceeds the time required for the necessary operation to be performed. Coherence times can be improved for a given modality by devising better protections for the qubit from the surrounding environment.

The gate fidelity corresponds to the error rate when performing gate operations. The higher the score, the better.

Gate time corresponds to the number of gate operations that can be performed before the qubit decoheres. The higher the score, the better.

Scalability corresponds to the number of qubits that can be successfully employed in a quantum computer, before the system’s functionality is impaired.

Quantum Error Correction corresponds to the ability for the system to correct errors, such as through using redundancy. As some number of a quantum computer’s qubits will be reserved for error correction, raw qubit counts are not a reliable means to understand the number of usable qubits available for your algorithm. Qubit Volume and algorithmic qubits give an indication of serviceable qubits (3, 4).

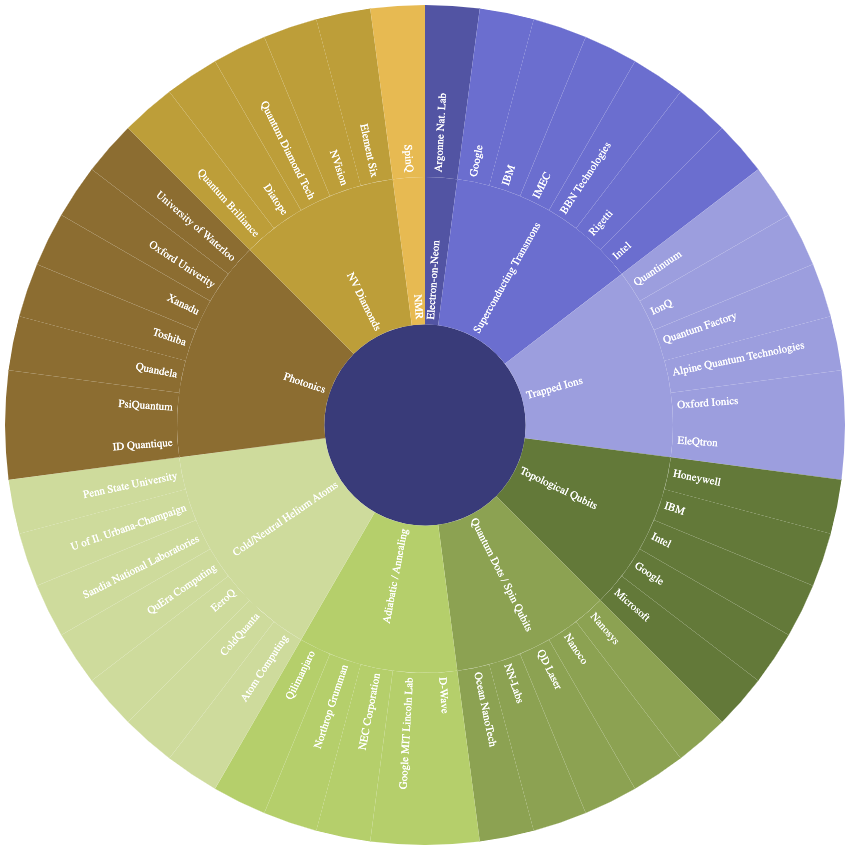
It remains to be seen which of these qubit modalities will prove to be the most useful for a given type of algorithm. For a detailed, informal consideration of qubit fidelity, see Jack Krupansky’s Nines of Qubit Fidelity. Below is a non-exhaustive representation of qubit modalities by organization.

Sourced from (1, 5).

New Electron-on-Neon Qubit Modality Announced by Argonne National Laboratory

Just last month, a very promising qubit modality joined the qubit platform race, and has the potential to leapfrog all the others. The new electron-on-neon qubit platform has the potential to become the first manifestation of an ideal qubit (5). Clearly, given the potential for low-cost fabrication, this could accelerate the timetable for practical quantum computers. Furthermore, it is likely to pave the way for other platforms, and further accelerate the quantum computing industry.

Beyond quantum computing, this solid-state single-electron qubit platform creates an appealing hybrid quantum framework that can connect various qubit platforms, thereby paving new pathways in quantum information science and technology. (6)

Quantum Computational Advantage

The ability to control individual quantum degrees of freedom and their interactions unlocks the capability to perform quantum coherent computation. (1)

Besides the qubit’s social predisposition for entangling with other qubits, it has an essence of freedom that no Woodstock or Burning Man participant could ever come close to matching—degrees of freedom. In physics, not surprisingly, a degree of freedom is something physical. It is an independent, physical phenomenon that can be represented as a parameter in a state space that can vary in value. In physics, this state space is often referred to as phase space. Due to the Uncertainty Principle, there is no straightforward and reliable way to measure these independent degrees of freedom at the same time. Measuring a single degree of freedom reduces the qubit to that one single, observed value.

This is the gist of the potential for quantum computational advantage, now being celebrated by the greatest realization of it yet with Xanadu’s bold demonstration using their newest photonic quantum computer, Borealis. Some modalities have more qubits, some have better connectivity between the qubits, or different gate fidelities and coherence times, and of course, different error rates. But as qubit count alone can’t accurately measure the performance of a quantum computer or its suitability to an application, the modality too cannot be the sole indicator of performance. – classiq.io

P-bits

Just beyond the qubit world, is another probabilistic, non-classical computing platform. Depending on the respective maturation timelines, p-bits could be an alternative, interim solution compared to qubits. Why? Because as nicely put by Kayla Wiles, Senior Science Writer at Purdue University, taking up Supriyo Datta’s poor man’s qubit moniker:

‘Poor man’s qubit’ can solve quantum problems without going quantum (7)

Supriyo Datta is the Thomas Duncan Distinguished Professor of Electrical and Computer Engineering at Purdue University, heading up p-bits research at Purdue University. This work goes back to collaborations with Kerem Camsari, Assistant Professor of Electrical and Computer Engineering at UC Santa Barbara, and Sayeef Salahuddin, TSMC Distinguished Professor at EECS, UC Berkeley, who all together had been exploring a new computing model characterized by “tunable” randomness (8).

P-bits, otherwise known as Probabilistic Bits, use magnets small enough to induce instability so that the attraction/repulsion fluctuates rapidly to create randomness. Unlike quantum computers, which use probability amplitudes, probabilistic computers use normal probabilities. As a result, p-bits do not utilize negative probabilities, thus probabilities cannot be made to cancel out as with quantum interference.

The power of quantum computing comes directly from this ability to negate probabilities. Celebrated quantum algorithms—like the one Peter Shor developed for integer factorization or the one Lov Grover devised for searching through data—carefully orchestrate the intermediate paths available so that those leading to the wrong outputs cancel, while those leading to the right answers add constructively. (2)

Additionally, though there is support for reversible circuits, it does not seem to be the case that probabilistic circuit operations are reversible in general, though that’s likely something that is doable. Still, p-bits seem to offer a compelling opportunity to explore probabilistic computing and reversibility.

The Social Qubit